2016/07/24
263697.- El Número "e"
Número e
La constante matemática e es el único número real tal que el valor de su derivada (la pendiente de su línea tangente) en la función f(x) = ex en el punto x = 0 es exactamente 1. La función ex es también llamada función exponencial y su función inversa es el logaritmo natural o también llamado logaritmo en base e.
El número e es uno de los números más importantes en la matemática, además de las identidades de la multiplicación y la suma del 0 y el 1, la unidad imaginaria i y π.
El número e es llamado ocasionalmente número de Euler, debido al matemático suizo Leonhard Euler, o también constante de Neper, en honor al matemático escocés John Napier, quien introdujo el concepto de logaritmo al cálculo matemático. (e no debe ser confundido con γ, la constante de Euler-Mascheroni, a la que a veces se hace referencia como constante de Euler)
El número e, base de los logaritmos naturales o neperianos, es sin duda el número más importante del campo del cálculo. Como e es un número trascendental, y por lo tanto es irracional, su valor no puede ser dado exactamente como un número finito o con decimales periódicos.
Su valor aproximado por truncamiento es:
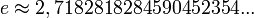
Las primeras referencias a la constante fueron publicadas en 1618 en la tabla en un apéndice de un trabajo sobre logaritmos de John Napier. No obstante, esta tabla no contenía el valor de la constante, sino que era simplemente una lista de logaritmos naturales calculados a partir de ésta. Se asume que la tabla fue escrita por William Oughtred. El "descubrimiento" de la constante está acreditado a Jacob Bernoulli, quien intentó encontrar el valor de la siguiente expresión (cuyo resultado, de hecho es e):

El primer uso conocido de la constante, representado por la letra b, fue en una carta de Gottfried Leibniz a Christiaan Huygens en 1690 y 1691. Leonhard Euler comenzó a utilizar la letra e para identificar la constante en 1727, y el primer uso de e en una publicación fue en Mechanica, de Euler, publicado en 1736. Mientras que en los años subsiguientes algunos investigadores usaron la letra c, e fue la más común, y finalmente se convirtió en la terminología usual.
La definición más común es la siguiente: e es el único número real cuyo logaritmo natural es 1:

Lo que significa:

EL NÚMERO E SEGÚN ADRIAN PAENZA
(realmente vale la pena leerlo) Quiero plantear aquí un problema que tiene que ver con poner dinero en un banco que rinda un determinado interés. Para hacer la exposición más clara, voy a tomar un ejemplo. Vamos a suponer que una persona tiene un capital de un peso. Y vamos a suponer también que el interés que le pagan anualmente por ese peso es del 100%. Ya sé... con este interés, uno sabe que el banco se funde antes de empezar y que el ejemplo está condenado al fracaso. Pero igualmente, síganme que es interesante.
Capital: 1 peso
Interés: 100% anual
Si uno hace la inversión en el banco y se va a su casa, ¿cuanto dinero tiene cuando vuelve justo al año? Claro, como el interés es del 100%, al año el señor tiene dos pesos: uno que corresponde a su capital y otro que es producto del interés que le pagó el banco. Hasta acá, todo claro:
Capital al cabo de un año: 2 pesos
Supongamos ahora que el señor decide poner su dinero no a un año, sino sólo a seis meses. El interés (a lo largo de todo este ejemplo) permanecerá constante: siempre será de un 100%. Al cabo de seis meses entonces, el señor ¿cuanto dinero tiene? ¿Está claro que tiene 1,5 pesos?
Esto es porque el capital permanece intocable: sigue siendo un peso. En cambio, como el interés es del 100% pero sólo dejó el dinero invertido la mitad del año, le corresponde un interés de la mitad de lo que invirtió y, por eso, le corresponden $ 0,50 de interés. Es decir, su nuevo capital es de $ 1,5. Si ahora el señor decide reinvertir su nuevo capital en el mismo banco, con el mismo interés (100%) y por otros seis meses de manera de llegar nuevamente al año como antes, ¿cuánto dinero tiene ahora?
Nuevo capital: 1,5
Interés: 100% anual
Plazo que lo deposita: 6 meses
Al finalizar el año, el señor tiene
1,5 + 1/2 x (1,5) = 2,25
¿Por qué? Porque el capital que tenía a los 6 meses iniciales, no se toca: $ 1,5. El nuevo interés que cobra es de la mitad del capital, porque el dinero lo pone a un interés del 100% pero sólo por seis meses. Por eso, tiene 1/2 x (1,5) = 0,75 como nuevo dinero que le aporta el banco como producto de los intereses devengados.
MORALEJA: al señor le conviene (siempre que el banco se lo permita) depositar el dinero primero a seis meses y luego renovar el plazo fijo a otros seis meses. Si comparamos con lo que le hubiera tocado en el primer caso, al finalizar el año tenia dos pesos. En cambio, reinvirtiendo en la mitad, al cabo de 365 días tiene $ 2,25.
Supongamos ahora que el señor coloca el mismo peso que tenía originalmente, pero ahora por cuatro meses. Al cabo de esos cuatro meses, reinvierte el dinero, pero por otros cuatro meses. Y finalmente, hace una última reinversión (siempre con el mismo capital) hasta concluir en el año. ¿Cuánto dinero tiene ahora?
Yo sé que ustedes pueden seguir leyendo en esta misma página y encontrar la solución, pero siempre es deseable que los lectores hagan un mínimo esfuerzo (si así lo desean) de pensar solos. De todas maneras, aquí va. Veamos si se entiende.
Al principio del año el señor tiene:
1
A los cuatro meses (o sea, transcurrido 1/3 del año) tiene:
(1 + 1/3)
A los siguientes cuatro meses (ocho desde el comienzo) tiene:
(1+1/3) + 1/3 (1+1/3) = (1+1/3) x (1+1/3) = (1+1/3) 2
(Esto sucede porque a los cuatro meses el capital es de (1+1/3) y al cabo de otros cuatro meses, tendrá el capital más un tercio de ese capital.
La cuenta que sigue después, (1+1/3) 2 , se obtiene de "sacar factor común" (1 +1 /3) en el término de la izquierda en la ecuación.
Ahora bien: cuando el señor invierte (1+1/3) 2 por otros cuatro meses, al llegar justo al fin del año, el señor tendrá el capital (1 +1/3) 2 más (1/3) de ese capital. O sea:
(1+1/3) 2 + 1/3(1+1/3) 2 = (1+1/3) 2 x (1+1/3) = (1+1/3) 3 = 2,37037037...
Como seguramente advierten, ahora nos queda la tentación de hacerlo no sólo cada cuatro meses, sino cada tres meses. Los invito a que hagan la cuenta ustedes, pero el resultado lo escribo yo. Al cabo de un año, el señor tendrá:
(1 + 1/4) 4 = 2,44140.625
Si lo hiciera cada dos meses, tendría que reinvertir su dinero seis veces en el año
(1 + 1/6) 6 = 2,521626372...
Si lo hiciera una vez por mes, reinvertiría doce veces por año
(1+1/2) 12 = 2,61303529...
Como usted ve, al señor le conviene poner su dinero a plazo fijo, pero hacerlo con un plazo cada vez más corto y reinvertir lo que obtiene (siempre con el mismo interés).
Supongamos que el banco le permitiera al señor renovar su plazo diariamente. En este caso, el señor tendría
(1 +1/365) 365 = 2,714567482...
Y si lo hiciera una vez por hora (como en el año hay 8.760 horas), tendría:
(1+1/8.760) 8.760 = 2,718126692...
Y si se le permitiera hacerlo una vez por minuto, como en el año hay 525.600 minutos, su capital resultaría
(1+1/525.600) 525.600 = 2,718279243
Y por último, supongamos que le permitieran hacerlo una vez por segundo.
En ese caso, como en el año hay 34.536.000 segundos, el capital que tendría al cabo de un año sería:
(1+1/34.536.000) 34.536.000 = 2,718281793...
MORALEJA: si bien uno advierte que el dinero al finalizar el año es cada vez mayor, sin embargo, el dinero que uno tiene al final no aumenta indiscriminadamente.
Voy a hacer un resumen de la lista que hemos escrito recién:
1 vez al año,
2 veces al año,
3 veces al año (cuatrimestral),
4 veces al año (trimestral),
6 veces al año (bimestral),
12 veces al año (mensual),
365 veces al año (diario),
8.760 veces al año (por minuto),
525.600 veces al año (una vez por minuto),
34.536.000 veces al año (una vez por segundo), 2
2,25
2,37037037...
2,44140625...
2,521626372...
2,61303529...
2,714567482...
2,718126692...
2,718279243...
2,718281793...
Lo que es muy interesante es que estos números, si bien crecen cada vez que el interés se cobra más frecuentemente, no lo hacen en forma ni arbitraria ni desbocada. Al contrario: tienen un tope, están acotados. Y la cota superior (es decir, si uno pudiera imaginariamente estar renovándolo instantáneamente) es lo que se conoce como el número e (que es la base de los logaritmos naturales, cosa que no importa en este contexto). No sólo es una cota superior, sino que es el número al cual se está acercando cada vez más la sucesión que estamos generando al modificar los plazos de reinversión.
El número e es un número irracional, cuyas primeras cifras decimales son:
e = 2,718281828...
El número e es uno de los números más importantes de la vida cotidiana, aunque su relevancia está generalmente escondida para el gran público. En algún otro momento y lugar, habría que divulgar mucho más sobre él. Por ahora, nos contentamos con celebrar su aparición en este escenario, mostrándolo como el límite (y también la cota superior) del crecimiento de un capital de $ 1 a un interés del 100% anual y renovado periódicamente.
FUENTE: http://es.wikipedia.org/wiki/N%C3%BAmero_e
y el libro "Matematica estas ahi?" de Adrian Paenza.
Suscribirse a:
Comentarios (Atom)



